https://doi.org/10.1140/epja/s10050-020-00303-9
Regular Article - Theoretical Physics
Some properties of Wigner 3j coefficients: non-trivial zeros and connections to hypergeometric functions
A tribute to Jacques Raynal
1
CEA, DAM, DIF, 91297, Arpajon, France
2
Université Paris-Saclay, CEA, Laboratoire Matière sous Conditions Extrêmes, 91680, Bruyères-le-Châtel, France
Received:
1
October
2020
Accepted:
6
November
2020
Published online:
23
November
2020
The contribution of Jacques Raynal to angular-momentum theory is highly valuable. In the present article, I intend to recall the main aspects of his work related to Wigner 3j symbols. It is well known that the latter can be expressed with a hypergeometric series. The polynomial zeros of the 3j coefficients were initially characterized by the number of terms of the series minus one, which is the degree of the coefficient. A detailed study of the zeros of the 3j coefficient with respect to the degree n for 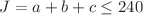 (a, b and c being the angular momenta in the first line of the 3j symbol) by Raynal revealed that most zeros of high degree had small magnetic quantum numbers. This led him to define the order m to improve the classification of the zeros of the 3j coefficient. Raynal did a search for the polynomial zeros of degree 1 to 7 and found that the number of zeros of degree 1 and 2 are infinite, though the number of zeros of degree larger than 3 decreases very quickly as the degree increases. Based on Whipple’s symmetries of hypergeometric
(a, b and c being the angular momenta in the first line of the 3j symbol) by Raynal revealed that most zeros of high degree had small magnetic quantum numbers. This led him to define the order m to improve the classification of the zeros of the 3j coefficient. Raynal did a search for the polynomial zeros of degree 1 to 7 and found that the number of zeros of degree 1 and 2 are infinite, though the number of zeros of degree larger than 3 decreases very quickly as the degree increases. Based on Whipple’s symmetries of hypergeometric 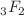 functions with unit argument, Raynal generalized the Wigner 3j symbols to any arguments and pointed out that there are twelve sets of ten formulas (twelve sets of 120 generalized 3j symbols) which are equivalent in the usual case. In this paper, we also discuss other aspects of the zeros of 3j coefficients, such as the role of Diophantine equations and powerful numbers, or the alternative approach involving Labarthe patterns.
functions with unit argument, Raynal generalized the Wigner 3j symbols to any arguments and pointed out that there are twelve sets of ten formulas (twelve sets of 120 generalized 3j symbols) which are equivalent in the usual case. In this paper, we also discuss other aspects of the zeros of 3j coefficients, such as the role of Diophantine equations and powerful numbers, or the alternative approach involving Labarthe patterns.
© Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2020




