https://doi.org/10.1140/epja/s10050-024-01373-9
Regular Article - Theoretical Physics
Demonstration of the rodeo algorithm on a quantum computer
1
Department of Physics and Astronomy, Facility for Rare Isotope Beams, Michigan State University, 48824, East Lansing, MI, USA
2
Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, 02139, Cambridge, MA, USA
Received:
30
December
2023
Accepted:
1
July
2024
Published online:
20
July
2024
The rodeo algorithm is an efficient algorithm for eigenstate preparation and eigenvalue estimation for any observable on a quantum computer. This makes it a promising tool for studying the spectrum and structure of atomic nuclei as well as other fields of quantum many-body physics. The only requirement is that the initial state has sufficient overlap probability with the desired eigenstate. While it is exponentially faster than well-known algorithms such as phase estimation and adiabatic evolution for eigenstate preparation, it has yet to be implemented on an actual quantum device. In this work, we apply the rodeo algorithm to determine the energy levels of a random one-qubit Hamiltonian, resulting in a relative error of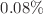 
using mid-circuit measurements on the IBM Q device Casablanca. This surpasses the accuracy of directly-prepared eigenvector expectation values using the same quantum device. We take advantage of the high-accuracy energy determination and use the Hellmann–Feynman theorem to compute eigenvector expectation values for a different random one-qubit observable. For the Hellmann–Feynman calculations, we find a relative error of 
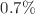. We conclude by discussing possible future applications of the rodeo algorithm for multi-qubit Hamiltonians.
Supplementary Information The online version contains supplementary material available at https://doi.org/10.1140/epja/s10050-024-01373-9.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2024. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
