https://doi.org/10.1140/epja/s10050-025-01496-7
Regular Article - Theoretical Physics
Negative moments as the signature of the radial density at small distances
Université Paris-Saclay, CNRS/IN2P3, IJCLab, 91405, Orsay, France
Received:
21
June
2024
Accepted:
21
January
2025
Published online:
8
February
2025
The present paper proposes a robust evaluation of any radial density at small distances using negative-order radial moments evaluated in momentum space. This evaluation provides a valuable insight into the behavior of a given radial density in the vicinity of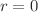 
, and puts strong emphasis on the importance of measuring form factors at large squared four-momentum transfer, a domain essential for the determination of negative order moments. A specific attention is paid to the regularization scheme directly affecting the numerical determination of the radial density’s parametrization. The proposed method is applied to non-relativistic study cases of the nucleon electric (
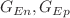), and proton magnetic 
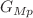form factors. The validation is performed through comparison of the results of the approach to the analytically determined Maclaurin expansion - in the vicinity of 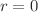- of the radial density function. The method is also applied to the relativistic Dirac form factor 
of the proton. In such a non-trivial case, the Maclaurin development might not exist for the radial density, rendering the determination from the proposed method extremely important.
© The Author(s) 2025
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
