https://doi.org/10.1140/epja/s10050-023-01196-0
Regular Article - Theoretical Physics
Universality of three identical bosons with large, negative effective range
1
Institute for Nuclear Studies, Department of Physics, The George Washington University, 20052, Washington, DC, USA
2
Université Paris-Saclay, CNRS/IN2P3, IJCLab, 91405, Orsay, France
3
Department of Physics, University of Arizona, 85721, Tucson, AZ, USA
Received:
10
August
2023
Accepted:
14
November
2023
Published online:
11
December
2023
“Resummed-Range Effective Field Theory” is a consistent nonrelativistic Effective Field Theory of contact interactions with large scattering length a and an effective range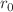 
large in magnitude but negative. Its leading order is non-perturbative, and its observables are universal in the sense that they depend only on the dimensionless ratio 
once the overall distance scale is set by 
. In the two-body sector, the relative position of the two shallow S-wave poles in the complex plane is determined by 
. We investigate three identical bosons at leading order for a two-body system with one bound and one virtual state (
), or with two virtual states (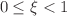
). Such conditions might, for example, be found in systems of heavy mesons. We find that no three-body interaction is needed to renormalise (and stabilise) the leading order. A well-defined ground state exists for 
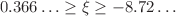. Three-body excitations appear for even smaller ranges of around the “quasi-unitarity point”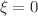 
(
) and obey discrete scaling relations. We explore in detail the ground state and the lowest three excitations. We parametrise their trajectories as function of and of the binding momentum 
of the shallowest 
state. These stretch from the point where three- and two-body binding energies are identical to the point of zero three-body binding. As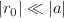 
becomes perturbative, this version turns into the “Short-Range EFT” which needs a stabilising three-body interaction and exhibits Efimov’s Discrete Scale Invariance. By interpreting that EFT as a low-energy version of Resummed-Range EFT, we match spectra to determine Efimov’s scale-breaking parameter 
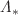in a renormalisation scheme with a “hard” cutoff. Finally, we compare phase shifts for scattering a boson on the two-boson bound state with that of the equivalent Efimov system.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2023. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
