https://doi.org/10.1140/epja/s10050-024-01267-w
Regular Article - Theoretical Physics
Variational calculations of symmetric nuclear matter and pure neutron matter with the tensor-optimized Fermi Sphere (TOFS) method: many-body effects and short-range correlation
Faculty of Science and Engineering, Kanto Gakuin University, 236-8501, Yokohama, Japan
Received:
30
December
2023
Accepted:
9
February
2024
Published online:
11
March
2024
The equations of state for symmetric nuclear matter and pure neutron matter are investigated with the tensor-optimized Fermi Sphere method (TOFS) up to the density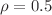 
fm
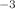. This method is based on a linked-cluster expansion theorem, and the energy per particle of nuclear matter (
) is calculated variationally with respect to the correlated nuclear matter wave function. We can study the density dependence of the many-body terms arising from the operator products, which contribute to . In order to clarify the relation between the many-body effects and short-range correlation, we take the spin-isospin dependent central NN interaction with a few GeV repulsion in the inner region. The EOS obtained by the TOFS method is reasonably reproduced, compared with other ab initio many-body methods. We found that the many-body terms (from the 2-body to 6-body ones) give sizable effects on E/A at higher density, and they play an important role in nuclear matter.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2024. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
